Tại sao a mũ 0 bằng 1? Lý do và ứng dụng trong toán học
admin-gocgiaidap March 19, 2025Giải Đáp ArticleGiới Thiệu
Trong toán học, một trong những quy tắc căn bản nhất về lũy thừa là: với mọi số thực a ≠ 0, ta có a0 = 1. Quy tắc này không chỉ được áp dụng rộng rãi trong các bài toán mà còn là nền tảng của nhiều lý thuyết số học hiện đại. Bài viết này sẽ giúp bạn hiểu sâu hơn về lý do tại sao a mũ 0 bằng 1 thông qua các định nghĩa, quy tắc và ví dụ minh họa cụ thể.
Tại Góc Giải Đáp, chúng tôi luôn nỗ lực mang đến những thông tin chính xác, bổ ích về các khái niệm toán học. Album “Giải Đáp” cũng thường xuyên cập nhật các kiến thức mới, giúp bạn nâng cao hiểu biết về các quy tắc số học cơ bản.

Bảng lũy thừa của một số cơ bản
1. Khái Niệm và Định Nghĩa
1.1. Định Nghĩa Lũy Thừa
Lũy thừa là phép toán biểu diễn việc nhân một số với chính nó nhiều lần. Cụ thể, với số mũ n, ta có:
an = a × a × … × a
(n lần)
Trong đó, a được gọi là cơ số và n là số mũ.
1.2. Định Nghĩa của a0
Theo định nghĩa của lũy thừa, khi số mũ bằng 0, ta cần đưa ra quy tắc đặc biệt. Dựa trên các định lý và tính chất của lũy thừa, đối với bất kỳ số thực a ≠ 0, ta có:
a0 = 1
Đây là quy tắc mà hầu hết các sách toán cơ bản đều công nhận.
2. Lý Do và Cơ Sở Toán Học
2.1. Tính Chất của Lũy Thừa
Để hiểu tại sao a0 = 1, hãy xem xét tính chất của lũy thừa, đặc biệt là tính chất của phép chia:
am ÷ an = am-n (với a ≠ 0)
Nếu ta lấy m = n, ta có:
an ÷ an = an-n = a0
Vì vậy, do an ÷ an = 1, nên a0 = 1.
2.2. Ví Dụ Minh Họa
Nếu a = 5 và n = 3, ta có:
53 ÷ 53 = 53-3 = 50 = 1
Như vậy, với bất kỳ giá trị nào của a (không bằng 0), quy tắc luôn cho ra kết quả 1.
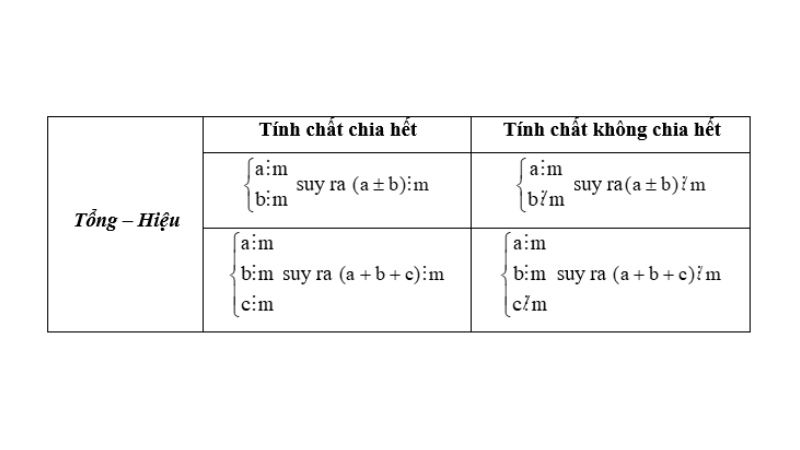
Quy tắc chia hai lũy thừa cùng cơ số
3. Các Phương Pháp Chứng Minh Khác
3.1. Suy Diễn Từ Định Nghĩa Ban Đầu
Nếu mở rộng định nghĩa của lũy thừa cho số mũ là số nguyên dương:
an = a × a × … × a
Để duy trì tính nhất quán, ta cần một giá trị cho a0 sao cho:
a0 × an = a0+n = an
Điều này chỉ xảy ra khi a0 = 1.
3.2. Kết Luận Từ Tính Chất Đối Xứng
Tính chất đối xứng của lũy thừa cho thấy:
a1 = a, a0 = a ÷ a = 1
Mỗi khi số mũ giảm một đơn vị, ta chia cho a. Khi đạt đến 0, ta có a0 = 1.
Xem thêm: Số nguyên là gì? Định nghĩa, tính chất và ứng dụng
4. Ứng Dụng và Ý Nghĩa của Quy Tắc a0 = 1
4.1. Vai Trò trong Toán Học
Quy tắc a0 = 1 giúp đơn giản hóa các biểu thức toán học, đặc biệt trong đại số và giải tích. Nó còn là nền tảng cho nhiều lý thuyết phức tạp như chuỗi số và hàm mũ.
4.2. Ứng Dụng trong Khoa Học và Kỹ Thuật
Quy tắc này được áp dụng trong lập trình và vật lý để đảm bảo tính nhất quán của các công thức và phép tính.
4.3. Ví Dụ Minh Họa
Trong kinh tế học, lãi suất kép được tính theo công thức:
A = P(1 + r)n
Khi n = 0:
A = P(1 + r)0 = P
Điều này cho thấy nếu không có thời gian trôi qua, số tiền gốc không thay đổi – khẳng định rằng a0 = 1.

Công thức lãi suất kép trong tài chính
5. Kết Luận
Quy tắc a0 = 1 là nền tảng quan trọng trong toán học, giúp đơn giản hóa biểu thức và xây dựng lý thuyết phức tạp. Hiểu rõ quy tắc này giúp người học nhận thức sâu sắc về mối liên hệ giữa các phép toán và ứng dụng của chúng trong đời sống.
Nếu bạn quan tâm đến các chủ đề về toán học, khoa học và kiến thức nền tảng, hãy theo dõi Góc Giải Đáp và album “Giải Đáp” để nhận thêm nhiều bài viết chất lượng. Chia sẻ bài viết với bạn bè và người thân để cùng nhau lan tỏa kiến thức bổ ích và cập nhật những thông tin mới nhất!
Xem thêm:
-
Hộ kinh doanh đóng thuế như thế nào? Hướng dẫn chi tiết
-
Vì sao giá trị đồng Yên giảm? – Phân tích nguyên nhân và xu hướng
You may also like
Archives
Calendar
| M | T | W | T | F | S | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | ||||||